Россия в глобальной политике

В издательстве «Бомбора» готовится к выходу книга математика и биолога Кита Йейтса «Математика жизни и смерти». Мы предлагаем вашему вниманию самые интересные и познавательные выдержки из неё, посвящённые математике эпидемий. Благодарим издательство за любезное разрешение опубликовать этот материал.

Инфекционные болезни сопровождают род людской большую часть его существования. Более 5000 лет назад значительную часть населения Древнего Египта поразили малярия и туберкулез. «Юстинианова чума» с 541 по 542 гг. выкосила от 15 до 25% населения мира, насчитывавшего тогда 200 млн человек. После вторжения Кортеса в Мексику местное население сократилось с примерно 30 млн в 1519 г. до 3 млн 50 лет спустя; ацтеки не могли сопротивляться болезням, принесённым западными конкистадорами. Список этот можно продолжить.

Даже сегодня, при достаточно развитом здравоохранении, большинство людей почти ежегодно сталкиваются с банальной простудой и гриппом. Холера или туберкулез в развитом мире встречаются реже, но во многих странах Африки и Азии они не редкость.

В борьбе с крупномасштабными инфекциями решающую роль играет математическая эпидемиология. Математика находится в центре жизненно важных мероприятий, призванных избавить Землю от болезней – начиная с выявления рисков, которым грозит человечеству набирающее мощь движение против вакцинации, и заканчивая борьбой с глобальными пандемиями.

Оспа

К середине XVIII в. оспа была распространена повсеместно. Считается, что только в Европе от этой болезни умирало 400 тыс. человек в год, что составляло до 20% всех смертей на континенте. Работая врачом в сельской местности Глостершира, Эдвард Дженнер пришёл к выводу, что лёгкая коровья оспа, которой заражалось большинство доярок, обеспечивает некоторый иммунитет от оспы натуральной – человеческой.

В 1796 г. Дженнер провёл эксперимент, который сегодня считался бы дико неэтичным. Он втёр гной из язвочки на руке доярки, заражённой коровьей оспой, в порез на руке восьмилетнего Джеймса Фиппса. У мальчика быстро появились высыпания и развилась лихорадка, но через десять дней он встал на ноги, такой же здоровый, как и до прививки. Два месяца спустя Дженнеру привил мальчику более опасный штамм человеческой оспы. Прошло несколько дней, но у Фиппса не появились симптомы болезни, и Дженнер пришёл к выводу, что у того выработался иммунитет. Дженнер назвал свой защитный процесс «вакцинацией», от латинского слова vaccas – корова. По словам Дженнера, «конечным результатом этой практики должно стать уничтожение оспы». Почти 200 лет спустя, в 1977 г., благодаря напряжённой работе Всемирной организации здравоохранения по вакцинации мечта Дженнера стала реальностью.

Корни математической эпидемиологии также связаны с попыткой побороть оспу, но происхождением своим эта наука обязана не только Дженнеру.

Задолго до того, как Дженнеру в голову пришла идея вакцинации, народы Индии и Китая практиковали вариоляцию. Для предотвращения оспы люди вдыхали перетертые в пыль струпья переболевших или вводили их гной в порез на руке, чтобы спровоцировать у себя более мягкую форму оспы, которая, хотя и неприятна, но гораздо менее опасна и обеспечит пациенту пожизненный иммунитет. Эта практика быстро распространилась на Ближнем Востоке, а затем, в начале 1700-х гг., и в Европе.

В некоторых случаях она не защищала пациентов от повторного, более серьёзного приступа оспы по мере ослабления иммунитета. Кроме того, 2% из тех, кто подвергся вариоляции, умирали. И хотя это значительно меньше, чем смертность в 20–30% при естественном заражении, критики утверждали, что многие пациенты, подвергшиеся вариоляции, возможно, никогда не заразились бы оспой, поэтому широкая профилактика является ненужным риском. Отмечалось также, что после вариоляции больные могли распространять заболевание так же эффективно, как и те, кто инфицировался естественным образом. В отсутствие контролируемых медицинских испытаний количественная оценка вариоляции и её научная реабилитация были практически недостижимы.

Именно эта проблема заинтересовала швейцарского математика Даниила Бернулли. Для определения общей эффективности вариоляции он предложил уравнение, которое описывало долю людей в каждой возрастной группе, никогда не болевших оспой и, следовательно, рискующих ею заразиться. Свое уравнение он выверял по таблице смертности[1], составленной Эдмундом Галлеем (прославившегося наблюдением за кометами), которая описывала, какая часть из всех родившихся доживала до определённого возраста. На этой основе Бернулли смог вычислить соотношение выздоровевших и умерших к общему числу тех, кто болел оспой. С помощью второго уравнения он подсчитал число жизней, которые могли бы быть спасены, если бы вариоляции регулярно подвергали всё население. Бернулли пришёл к выводу, что при всеобщей вариоляции почти 50% новорожденных доживали бы до 25 лет. По сегодняшним меркам число удручающее, но по сравнению с показателем в 43% при свободном распространении оспы это существенный прогресс. Он также показал, что прививка способна увеличить среднюю ожидаемую продолжительность жизни более чем на три года. Для Бернулли необходимость государственной медицинской программы борьбы с оспой была очевидна.

Модель SIR

В конце XIX века вспышка чумы в Индии привела к одному из самых важных открытий в истории эпидемиологии. Никто не знает точно, как эта болезнь попала в Бомбей в августе 1896 года. Наиболее вероятным объяснением, похоже, является то, что на борту торгового судна, прибывшего в Бомбей из британской колонии в Гонконге, оказались крысы, «перевозившие» блох, ответственных за распространение бактерии Yersinia pestis – чумы.

К маю 1897 г. жёсткие меры по сдерживанию распространения чумы, казалось, затушили пожар эпидемии. Однако в течение следующих 30 лет болезнь периодически возвращалась в Индию, убив более 12 млн человек.

В разгар одной из таких вспышек в 1901 г. в Индию прибыл молодой шотландский военный врач Андерсон Маккендрик. За 20 лет, проведённых в Индии, он изучил инфекционные заболевания, которые могут передаваться от животных людям. Вернувшись в Шотландию, Маккендрик занял должность руководителя лаборатории Королевской медицинской коллегии Эдинбурга. Там он познакомился с биохимиком Уильямом Кермаком. Воспользовавшись данными о чуме в Бомбее, собранными Маккендриком в Индии, они создали одну из первых математических моделей распространения инфекционных болезней. Они разделили население на три основные категории в соответствии со статусом заболевания. Тех, кто ещё не заболел, назвали «восприимчивыми» (Susceptible). Предполагалось, что восприимчивыми и способными к заражению рождаются все. Те, кто заразился и был способен передать болезнь восприимчивым, были названы «инфицированными» (Infected). В третью группу, названную «выбывшие» (removed), входили и те, кто переболел и приобрел иммунитет, и те, кто не справился с инфекцией и умер. Во всяком случае, выбывшие больше не способствовали распространению болезни. Это классическое математическое представление распространения инфекции называется моделью SIR.

Кермак и Маккендрик продемонстрировали функциональность SIR-модели, показав, что она точно воссоздает динамику заболевания чумой во время вспышки 1905 г. в Бомбее. За 90 лет с момента создания SIR-модель (и её модификации) успешно применялась для описания и профилактики всевозможных заболеваний – от лихорадки денге в Латинской Америке до европейской чумы свиней в Нидерландах и норовируса (желудочного гриппа) в Бельгии.

Презентеизм, предсказания и проблема чумы

Распространение так называемых «нулевых трудовых договоров»[2] и рост временной занятости – отличительная черта развивающейся «сдельной» экономики[3] – способствовали тому, что люди всё чаще приходят на работу больными. «Абсентеизм» (а проще – прогулы) изучался долго и обстоятельно, а вот то, во что обходится «презентеизм»[4], стало понятно относительно недавно. Исследования, сочетающие математическое моделирование и данные о фактическом присутствии на работе, позволили сделать некоторые удивительные выводы.

Проблема презентеизма особенно распространена в здравоохранении и образовании. По иронии судьбы, чувство долга медсестёр, врачей и учителей по отношению к тому множеству людей, которые от них зависят, часто заставляет их подвергать этих людей риску. Однако в наиболее острой форме презентеизм проявляется в ресторанно-гостиничном хозяйстве. Одно из исследований показало, что только в США с 2009 по 2012 год 70% вспышек норовируса были связаны с болезнями работников пищевой промышленности.

Через пять лет после завершения этого исследования пагубные последствия презентеизма испытала на себе сеть мексиканских гриль-баров Chipotle. С 2013 по 2015 год Chipotle считался сильнейшим мексиканским ресторанным брендом в США. Несмотря на то, что в компании действовала политика оплачиваемых больничных, работники многих филиалов Chipotle по всей территории США жаловались на то, что менеджеры под угрозой увольнения требовали, чтобы они приходили на работу даже нездоровыми.

14 июля 2017 г. Пол Корнелл решил отведать буррито в Стерлинге, ресторанчике сети Chipotle в штате Вирджиния. В тот же вечер оставшийся неназванным служащий этого ресторанчика вышел на работу, невзирая на резь в желудке и тошноту. Двадцать четыре часа спустя Корнелл оказался в больнице под капельницей – он страдал от сильных болей в животе, тошноты, диареи и рвоты, характерных для острой норовирусной инфекции. Всего вирус поразил сто тридцать пять человек, включая сотрудников и клиентов этого ресторана. За пять дней после вспышки заболевания акции Chipotle с грохотом обрушились, компания потеряла более миллиарда долларов рыночной стоимости, а собственные акционеры подали против неё коллективный иск. К концу 2017 г. сеть Chipotle болталась где-то в нижней половине списка самых популярных мексиканских ресторанных сетей Америки.

Модель SIR иллюстрирует, как важно воздержаться от выхода на работу в случае недомогания.

Оставаясь дома до полного выздоровления, вы переводите себя из категории инфицированных в категорию выбывших. Модель демонстрирует, что это простое действие может уменьшить масштаб эпидемии, снижая возможность передачи инфекции тем, кто к ней восприимчив.

Однако главное достоинство модели SIR состоит, пожалуй, в её прогностических возможностях. Она позволила Кермаку и Маккендрику предсказать взрывную динамику эпидемий и понять порой загадочные закономерности развития болезней. Так, острые дебаты вызывал вопрос «что вызывает затухание эпидемии?». Неужели болезнь просто заражает всё население, и когда инфицированными оказываются все, заразе просто некуда распространяться? Или же, возможно, патоген, вызывающий болезнь, с течением времени теряет силу до такой степени, что оказывается не способен инфицировать здоровых людей?

Шотландские учёные смогли показать, что ни один из этих исходов не является обязательным. Оценив состояние опытной популяции в конце смоделированной эпидемии, они обнаружили, что в ней всегда оставались несколько восприимчивых особей. Возможно, это противоречит нашему интуитивному пониманию, подталкивающему к мысли о том, что болезнь исчезает, потому что больше не осталось тех, кто мог бы заразиться. На деле же, по мере того как инфицированные восстанавливаются или умирают, контакты между оставшимися инфицированными и восприимчивыми людьми становятся настолько редкими, что у инфицированных не остаётся шанса заразить кого-либо до того, как они сами перейдут в категорию выбывших. Модель SIR предсказывает, что в конечном счёте вспышки угасают из-за уменьшения числа инфицированных, а не от недостатка восприимчивых.

Модель SIR Кермака и Маккендрика подняла изучение инфекционных болезней высоко над уровнем прежних, чисто описательных исследований, и позволила заглянуть в будущее. Тем не менее многочисленные допущения ограничивали область её применения весьма специфическими ситуациями. Подразумевалось, что скорость передачи болезни от человека к человеку постоянна; что инфицирование происходит мгновенно; что численность населения остаётся неизменной. Хотя в отдельных случаях эти допущения были полезны для описания некоторых болезней, для большинства они не годились.

Так, по иронии судьбы, данные по Бомбейской чуме, которые Кермак и Маккендрик использовали для валидации своей модели, ломают многие из этих предположений. В первую очередь, Бомбейская чума не передавалась от человека к человеку, а распространялась крысами, несущими блох, которые, в свою очередь, несли чумную бактерию. Модель SIR также предполагала постоянную скорость передачи инфекции между инфицированными и восприимчивыми. Фактически же распространение чумы в Бомбее было подвержено влиянию фактора сезонности: с января по март число блох и бактерий резко возрастало, что вело к увеличению скорости передачи.

Следующие поколения математиков адаптируют фундаментальную модель SIR, ослабляя её ограничительные допуски и расширяя спектр болезней, понять тайны которых помогла бы математика.

Нулевой пациент

Однажды днём в конце 2013 г. двухлетний Эмиль Уамуно играл с другими детьми в отдалённой гвинейской деревне Мелианду. Идеальным укрытием для игры в прятки было огромное дуплистое дерево кола на окраине деревни. Но глубокая и темная полость дерева служила обиталищем для популяции насекомоядных мешкокрылых летучих мышей. Играя на дереве, заселённом летучими мышами, Эмиль соприкасался либо с продуктами их жизнедеятельности, либо лицом к лицу с самими летунами.

2 декабря у мальчика начался жар, затем рвота и черный понос. Через четыре дня он умер. Его мать заразилась от сына и через неделю умерла. За ней последовала сестра Эмиля и его бабушка. Деревенская акушерка, которая ухаживала за семьёй, перенесла болезнь в соседние деревни. Зараза продолжала распространяться.

18 марта число случаев и масштабы заражения стали вызывать серьёзную тревогу. Медицинские чиновники публично объявили о вспышке геморрагической лихорадки неизвестного типа. Через две недели, идентифицировав заболевание как лихорадка Эбола, «Врачи без границ» назвали масштабы её распространения «беспрецедентными».

Метод, известный как «контактное отслеживание», позволяет проследить историю развития заболевания ретроспективно через многие поколения инфицированных, вплоть до исходного случая – нулевого пациента. Обратившись к инфицированным с просьбой перечислить всех, с кем они контактировали во время и после инкубационного периода учёные могут выстроить картину контактной сети пациента.

На практике, однако, контактные сети часто оказываются неполными, и многие носители инфекции остаются неизвестны. А многие даже не знают, что больны. В случае с лихорадкой Эбола инкубационный период может длиться до трёх недель, но в среднем составляет около 12 дней. В октябре 2014 г. стало ясно, что эпидемия в Западной Африке может приобрести глобальные масштабы. Правительство Великобритании под предлогом защиты своих граждан объявило о том, что пассажиров, въезжающих в Великобританию из стран с высоким уровнем риска, будут проверять на заболевание лихорадкой Эбола в пяти крупных аэропортах страны и в терминале поезда «Евростар» в Лондоне.

Аналогичная программа в Канаде во время эпидемии атипичной пневмонии в 2004 г. охватила почти полмиллиона путешественников и обошлась канадскому правительству в 15 млн долларов. Оглядываясь назад, можно сказать, что скрининг атипичной пневмонии был бесполезной мерой, которая, возможно, успокоила общественность, но в целом оказалась неэффективной.

Группа математиков Лондонской школы гигиены и тропической медицины разработала простую математическую модель. Учитывая средний 12-дневный инкубационный период лихорадки Эбола и шесть с половиной часов полёта из Фритауна в Сьерра-Леоне в Лондон, математики подсчитали, что эти новые дорогостоящие меры могли бы выявить лишь около 7% носителей вируса Эбола. И деньги, возможно, было бы лучше потратить на решение гуманитарных проблем Западной Африки, чтобы ликвидировать источник проблемы, снизив таким образом риск передачи вируса в Великобританию. Это наилучший пример математического вмешательства – простого, решительного и основанного на фактах. Вместо того, чтобы строить догадки о том, насколько эффективными могут быть скрининговые меры, простое математическое описание ситуации может дать представление о сути происходящего и направить политику в нужное русло.

Индекс репродукции и экспоненциальный взрыв

Определить, разовьётся ли вспышка заболеваемости в масштабную эпидемию или выдохнется и забудется, можно с помощью всего одного показателя, уникального для каждого случая – базового показателя репродукции.

Давайте представим, что население на некой территории полностью восприимчиво к определённым болезням – как это было с коренными жителями Мезоамерики в 1500-х гг. до прибытия конкистадоров. Среднее число лиц, инфицированных одним носителем болезни, известно как «базовый показатель репродукции» и часто обозначается R0 (произносится «R-ноль»). Если болезнь имеет R0 менее единицы, то инфекция быстро сходит на нет, так как каждый инфицированный передаёт болезнь в среднем менее чем одному человеку. Вспышка не становится самоподдерживающейся. Если R0 больше единицы, то инфекция будет распространяться в геометрической прогрессии.

Так, атипичная пневмония (SARS) имеет базовый показатель репродукции 2. Нулевой пациент заражает двоих, каждый из которых распространяет болезнь ещё на двоих – и так далее. Если бы болезнь распространялась таким образом и далее, то через десять поколений вниз по цепочке прогрессии заразилось бы более 1000 человек. Ещё десять шагов – и число заражённых превысит миллион.

На практике экспоненциальный рост, прогнозируемый на основе базового показателя репродукции, редко поддерживается более чем на несколько поколений. Вспышки в конечном итоге достигают пика, а затем идут на спад из-за того, что контакты между инфицированными и восприимчивыми к вирусу людьми становятся реже.

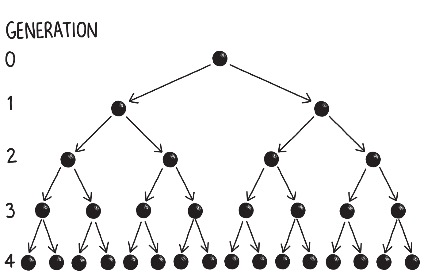
Рисунок 23: Экспоненциальное распространение болезни с базовым показателем репродукции R0 равным 2. Первое инфицированное лицо считается нулевым поколением. К четвёртому поколению инфицируются уже 16 человек.

Даже когда инфицированных не будет, и эпидемия официально закончится, некоторые восприимчивые к инфекции люди ещё останутся. В 1920-х гг. Кермак и Маккендрик предложили формулу, в которой базовый показатель репродукции использовался для предсказания числа восприимчивых, которые останутся незатронутыми инфекцией к завершению эпидемии. По этой формуле при R0 около 1,5 вспышка лихорадки Эбола в 2013–2016 гг. поразила бы 58% популяции, если бы не было принято никаких мер. Полиомиелит имеет R0 около 6, что, по прогнозам Кермака и Маккендрика, означает, что без вмешательства только четверть процента населения переживёт эпидемию, не заразившись.

Базовый показатель репродукции – универсальный индикатор для описания эпидемии. Он учитывает все её ключевые особенности и позволяет адекватно реагировать на неё. R0, как правило, можно разделить на три компонента: численность населения; скорость, с которой заражаются восприимчивые к инфекции люди; и срок выздоровления – или смерти от болезни. Увеличение первых двух факторов повышает R0, в то время как увеличение срока выздоровления уменьшает его. Чем больше население и чем быстрее болезнь распространяется, тем больше вероятность эпидемии. Чем быстрее люди выздоравливают, тем меньше времени они передают болезнь другим и, следовательно, тем меньше вероятность роста заболеваемости. Чаще всего мы можем контролировать только первые два фактора. Хотя антибиотики или противовирусные препараты могут сократить продолжительность некоторых болезней, скорость выздоровления или смертность часто являются свойством, присущим самому болезнетворному патогену. С показателем R0 тесно связана величина, называемая реальным коэффициентом репродукции (часто обозначается как Re) – среднее число вторичных инфекций, вызванных инфицированным лицом в определённый момент развития вспышки. Если медицинское вмешательство позволяет сбить значение Re ниже 1, то эпидемия утихнет.

Показатель R0 имеет решающее значение для борьбы с эпидемиями, но он не говорит, насколько болезнь опасна для инфицированного. Крайне заразное заболевание, такое как корь, например, имеющая показатель R0 от 12 до 18, обычно считается менее опасным, чем, допустим, лихорадка Эбола, у которой R0 составляет около 1,5. Корь распространяется быстро, но смертность от неё относительно низкая, особенно в сравнении с 50–70-процентной вероятностью смерти в случае лихорадки Эбола.

Заболевания, которые убивают большинство заражённых и при этом эффективно распространяются, очень редки. Чаще всего они встречаются в фильмах-катастрофах. Болезни с высоким R0, но с низким уровнем смертности, в конечном итоге могут оказаться более фатальными в силу того, что инфицируют больше людей.

Математика постулирует, что после принятия решения о начале борьбы с эпидемией, показатель уровня смертности не даёт полезной информации о том, как замедлить распространение болезни. Тем не менее три фактора, составляющие R0, подсказывают, какие меры стоит предпринять для того, чтобы остановить вспышки смертельных заболеваний прежде, чем они выйдут из-под контроля.

Укрощение эпидемий

Одним из наиболее эффективных способов снизить распространение инфекции является вакцинация. Перемещая людей из категории восприимчивых в категорию выбывших, минуя стадию инфицированности, она уменьшает размер популяции, восприимчивой к инфекции. Вакцинация, однако, является предупредительной мерой. Если же эпидемия уже началась, разработка и испытания вакцины в обозримый срок, как правило, уже нецелесообразны.

При эпидемиях у животных применяется стратегия, также понижающая значение реального коэффициента репродукции Re, – выбраковка. В 2001 г. в Великобритании забой заражённых ящуром особей позволил сократить инфекционный период с трёх недель до нескольких дней, что резко снизило реальный коэффициент репродукции.

Очевидно, что в случае активных вспышек человеческих болезней выбраковка – не вариант. Однако карантин и изоляция могут оказаться чрезвычайно эффективными способами снижения скорости передачи и, следовательно, реального коэффициента репродукции.

Оба действия способствуют снижению реального коэффициента репродукции. Так, последняя вспышка оспы в Европе, в Югославии в 1972 г., была быстро взята под контроль с помощью строжайшего карантина. До 10 тыс. потенциально инфицированных содержались под вооружённой охраной в гостиницах, реквизированных под эти цели, до тех пор, пока не исчезла угроза новых случаев заражения.

В менее экстремальных случаях наиболее эффективную продолжительность изоляции можно рассчитать при помощи математического моделирования. Математическая модель также может определить, следует ли перевести часть неинфицированного населения на карантин. Такое моделирование приходится очень кстати, когда проведение полевых исследований распространения болезни нецелесообразно по логистическим или этическим соображениям. Так, лишать какую-либо часть населения жизненно необходимой медицинской помощи во время вспышки заболевания просто бесчеловечно. Точно так же в реальном мире нецелесообразно помещать большую часть населения в карантин надолго. При использовании матмоделей таких проблем не возникает. При помощи математики можно протестировать модели тотального карантина – или полного отсутствия карантина, или какие-то промежуточные меры – в попытке сбалансировать экономические последствия вынужденной изоляции с тем влиянием, которое она окажет на распространение болезни.

 Математика показала, например, что при таких заболеваниях, как ветряная оспа, изоляция и карантин могут оказаться неправильным решением. Попытки изолировать больных детей, вне всякого сомнения, вынудят детей и взрослых массово пропускать занятия в школе и работу, чтобы избежать заболевания, которое считается относительно неопасным. Более того, математические модели доказывают, что здоровые дети, переживающие вспышки ветрянки на карантине, могут подхватить болезнь уже в старшем возрасте, когда осложнения, связанные с ветряной оспой, бывают гораздо более серьёзными.

Математические модели распространения инфекционных болезней выявили, что эффективность карантина зависит от времени пиковой инфекционности. Если болезнь особенно заразна на ранних стадиях, когда не появились симптомы, инфицированные могут распространить болезнь на большинство математически ожидаемых жертв, прежде чем их можно будет изолировать. К счастью, в случае с лихорадкой Эбола, при вспышке которой многие другие потенциальные пути контроля эпидемии недоступны, большинство случаев передачи инфекции происходит после того, как у заболевших проявляется симптоматика, так что их можно изолировать.

Фактически, контагиозный период лихорадки Эбола настолько долгий, что даже после смерти жертвы этой болезни остаются очень заразными.

В 2014 г., примерно в пиковый момент вспышки лихорадки Эбола, по результатам математического исследования был сделан вывод о том, что примерно 22% новых случаев заболевания вызваны контактами с трупами, умерших от лихорадки. Одной из наиболее важных мер, позволившей сократить базовый показатель репродукции вируса до значений, при которых эпидемия утратит способность к самоподдерживающемуся росту, стал запрет на традиционные похоронные процедуры и обеспечение безопасного и достойного захоронения всех жертв лихорадки. В сочетании с просветительскими кампаниями, рассказывающими об иных практиках, более безопасных, чем традиционные, и ограничениями на перемещение даже для на первый взгляд здоровых людей, вспышка лихорадки Эбола в конечном итоге была купирована. 9 июня 2016 г., спустя почти два с половиной года после заражения Эмиля Уамуно, было объявлено о завершении эпидемии лихорадки Эбола в Западной Африке.

Популяционный иммунитет

Помимо активной помощи в борьбе с эпидемиями, математические модели также могут объяснить необычные закономерности, свойственные различным заболеваниям. Так, ряд вопросов сформировался вокруг детских болезней, таких как свинка и краснуха: почему они поражают только детей? И почему эти болезни так долго сохраняются в нашем обществе?

Причина, по которой для детских заболеваний характерны периодические вспышки, заключается в том, что значение реального коэффициента репродукции с течением времени варьируется в зависимости от популяции восприимчивых к ним лиц. После того, как крупная вспышка скарлатины поразит значительную часть незащищённой популяции детей, она не просто исчезает. Она сохраняется в популяции, но её реальный коэффициент репродукции дрейфует в районе единицы. Со временем население стареет, и рождаются новые, незащищённые дети. По мере роста незащищённой части популяции реальный коэффициент репродукции растёт, что увеличивает вероятность новых вспышек. Когда болезнь, наконец, начинает распространяться, её жертвы, как правило, принадлежат к незащищённому молодому поколению. Те же, кто не переболел скарлатиной в детстве, как правило, получают определённую степень защиты от неё, поскольку они меньше общаются с представителями инфицированной возрастной группы.

Положение о том, что большое число людей с иммунитетом может замедлить или даже остановить распространение инфекции, как это происходит в периоды покоя между вспышками детских болезней, называется «популяционным иммунитетом». Опустив реальный коэффициент репродукции ниже единицы, можно разорвать цепь передачи инфекции и остановить распространение болезни. Популяционный иммунитет предполагает, что защита, которую обеспечивает вакцинация, в некоторой мере распространяется и на тех, у кого иммунная система слишком слаба, чтобы переносить прививки (включая пожилых, новорожденных, беременных и людей с ВИЧ). Это исключительно важно. Пороговое значение величины иммунной части населения, необходимое для защиты его восприимчивой части, варьируется в зависимости от того, насколько заболевание заразно. Ключом к тому, насколько эта доля велика, является базовый показатель репродукции R0.

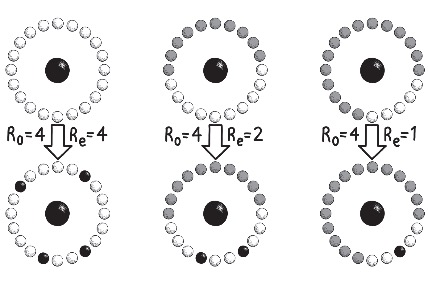
Рисунок 24: Один инфицированный (чёрный круг) сталкивается с 20 восприимчивыми (белый) или вакцинированными (серый) лицами в течение недельного инфекционного периода. Если не вакцинирован никто (слева), один заразившийся заражает четырех других, то еть базовый показатель репродукции R0 равен 4. При вакцинировании половины населения (в середине) заражаются только двое восприимчивых. Реальный коэффициент репродукции, Re, уменьшается до 2. Наконец (справа), когда вакцинировано 3/4 населения, в среднем заражается только один человек. Реальный коэффициент репродукции снижается до критического значения 1.

Возьмём, к примеру, человека, заражённого вирулентным штаммом гриппа. Если за неделю, столкнувшись с 20 восприимчивыми к вирусу людьми, он заразит четверых из них, то значение базового показателя репродукции заболевания R0 составит 4. У каждого восприимчивого человека шанс заразиться составляет один к пяти. Это демонстрирует, как показатель репродукции зависит от размера восприимчивой популяции. Если бы наш больной гриппом в течение недели, во время которой он остаётся носителем вируса, встречался только с десятью восприимчивыми к инфекции людьми (как на средней схеме на рис. 24), то при той же вероятности передачи, он заразил бы в среднем только двоих, понизив реальный коэффициент репродукции вдвое – с 4 до 2.

Наиболее эффективный способ сокращения численности восприимчивого населения – вакцинация. Число людей, которых нужно вакцинировать для достижения популяционного иммунитета, определяется задачей снизить реальный коэффициент репродукции ниже единицы. Если бы мы смогли вакцинировать 3/4 популяции, то (как в схеме справа на рис. 24) из первоначальных 20 контактов нашего больного за неделю, только 1/4 (то есть пятеро) всё равно были бы восприимчивы к инфекции. Из них, в среднем, заразился бы только один. Не случайно этот критический порог вакцинации для достижения популяционного иммунитета к заболеванию с базовым показателем репродукции 4 требует вакцинации трёх четвертей населения. В целом для достижения порога популяционного иммунитета мы можем позволить себе оставить 1/R0 популяции без вакцинации и должны защитить её оставшуюся долю (1 минус 1/R0 популяции). При оспе, базовый показатель репродукции которой составляет около 4, мы можем позволить себе оставить четверть (то есть 25%) популяции незащищённой. Вакцинации 80% (на 5% выше 75% критического порога иммунизации для обеспечения буфера) восприимчивого к оспе населения в 1977 г. хватило для того, чтобы стереть одну из человеческих болезней с лица Земли. Повторить этот подвиг не удалось.

Изнурительные и опасные последствия оспы сами по себе сделали её подходящей мишенью для искоренения. Низкий критический порог иммунизации сделал её ещё и относительно легкой мишенью. От многих других болезней защититься сложнее, так как они распространяются легче. Ветряная оспа, с оценочным R0 около 10, для эффективной защиты всего человечества – и последующего искоренения болезни – потребовала бы иммунизировать 9/10 населения Земли. Корь – безусловно, самая заразная болезнь человека на Земле, с оценочным R0 от 12 до 18 – потребует вакцинации от 92% до 95% населения.

Математическая эпидемиология предлагает стратегии борьбы со вспышками заболеваний и меры для их предотвращения. Она показывает, что вакцинация защищает не только вас, но и вашу семью, друзей, соседей и коллег. Данные Всемирной организации здравоохранения свидетельствуют, что вакцины ежегодно предотвращают миллионы смертей и могли бы предотвратить ещё больше, если бы мы смогли расширить глобальный охват вакцинирования. Прививки – лучший из имеющихся у нас способов избежать смертельных болезней и единственная возможность навсегда покончить с их разрушительными последствиями.